Dietrich

| Art |
Relikt |
|---|---|
| Index-Nr. |
149/166 |
| Seltenheit |
Legendär |
| Laden |
900 |
| Schwacher Fluch |
2 |
| Starker Fluch |
1 |
| Effekt |
Öffnet Schlösser kostenlos, aber wie lange noch? |
![]() Dietrich ist ein Relikt in UnderMine. Es kostet 2
Dietrich ist ein Relikt in UnderMine. Es kostet 2 ![]() Schwache Flüche und 1
Schwache Flüche und 1 ![]() Starken Fluch beim Sho'guuls Versteck.
Starken Fluch beim Sho'guuls Versteck.
Es öffnet Türen, Truhen und Blöcke, ohne die Schlüssel des Spielers zu verbrauchen. Jedes Mal, wenn es verwendet wird, steigt seine Wahrscheinlichkeit zu brechen um 2%; Die Chance (in Prozent) finden Sie im Reliktsymbol.
Es kann mit ![]() Glücksamulett kombiniert werden, um den
Glücksamulett kombiniert werden, um den ![]() Glücksdietrich zu erhalten.
Glücksdietrich zu erhalten.
Im Durchschnitt ist er etwa 9,5 Schlüssel wert (siehe Abschitt unten).
Die Chance, dass der Dietrich zerbricht, kann auf 0 zurückgesetzt werden, indem er auf den Reliktaltar gelegt und entfernt wird.
Interaktionen
Positiv
 Glücksamulett: Kombiniert sich zum
Glücksamulett: Kombiniert sich zum  Glücksdietrich.
Glücksdietrich.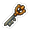 Schlüsselklinge: Je mehr Schlüssel behalten werden, desto mehr Schaden wird mit Schlüsselklinge verursacht.
Schlüsselklinge: Je mehr Schlüssel behalten werden, desto mehr Schaden wird mit Schlüsselklinge verursacht.
Statistische Analyse des Dietrichs
Eine statistische Analyse ist nützlich, um festzustellen, wie viele Schlüssel das Auffinden des Dietrichs Ihnen erspart. In den folgenden Abschnitten werden die Herleitung und die Schritte zur Ermittlung der statistischen Daten des Gegenstands erläutert.
Ableitung der Wahrscheinlichkeitsdichtefunktion
X sei die Anzahl der Schlüssel, die der Bauer mit dem Dietrich retten kann. Da der Dietrich dem Bauern einen Schlüssel rettet, auch wenn er zerbricht, ist die minimale Anzahl der geretteten Schlüssel 2 und die maximale Anzahl der geretteten Schlüssel 51.
Daher ist X = {2, 3, ..., 50, 51}.
Um die durchschnittliche Anzahl von Schlüsseln zu bestimmen, die der Bauer mit dem Dietrich retten kann, muss eine Wahrscheinlichkeitsdichtefunktion (PDF) gefunden werden. Um diesen Ausdruck abzuleiten, sei f(X) die Wahrscheinlichkeit, dass der Dietrich bei einer Anzahl von X geretteten Schlüsseln bis zur Bruchstelle nicht bricht. Analog dazu sei g(X) die Wahrscheinlichkeit, dass der Dietrich bei einer Anzahl von X gespeicherten Schlüsseln bricht. Im Folgenden wird eine Tabelle mit f(X) und g(X) für frühe Werte von X erstellt.
| X | f(X) | g(X) |
|---|---|---|
| 2 | 1 | 0.02 |
| 3 | 0.98 | 0.04 |
| 4 | 0.96 | 0.06 |
| ... | ||
| 49 | 0.06 | 0.96 |
| 50 | 0.04 | 0.98 |
| 51 | 0.02 | 1.00 |
Aus der Tabelle lässt sich leicht eine lineare Beziehung zwischen den Wahrscheinlichkeiten des Aufbrechens (oder Nichtaufbrechens) und der Anzahl der Schlüssel, die der Bauer mit dem Dietrich gerettet hat, erkennen. Diese Beziehungen lassen sich wie folgt ausdrücken:
Da nun die Wahrscheinlichkeiten für das Brechen und Nicht-Brechen für die Anzahl der gesicherten Schlüssel bekannt sind, ist es möglich, die PDF für die Anzahl der gesicherten Schlüssel abzuleiten. Die Wahrscheinlichkeit, X Schlüssel zu retten, ist gleich der Wahrscheinlichkeit, dass der Dietrich X-1 Mal überlebt und beim X-ten Versuch bricht.
Eine schnelle Überprüfung der Summe der Wahrscheinlichkeiten über den gesamten Stichprobenraum zeigt, dass die Wahrscheinlichkeit aller Ereignisse 1 ist:
Mittelwert und Varianz
Da nun die PDF der Anzahl der gespeicherten Schlüssel bekannt ist, müssen nur noch die Definitionen von Mittelwert und Varianz angewendet werden.
Der Mittelwert wird wie folgt berechnet:
Die Abweichung wird wie folgt berechnet:
Die Anwendung dieser Definitionen führt zu folgenden Ergebnissen:
Mit dem Dietrich spart der Bauer also im Durchschnitt 9,5 Schlüssel.
Geschichte
| Geschichte | |
|---|---|
| Version | Neuerungen und Änderungen |
| 0.3.0 |
|
| 0.3.1 |
|
Anmerkungen
- Ersetzt nicht die schlüsselbasierte Zahlung, wenn Sie etwas von Black Rabbit kaufen.



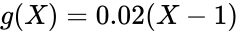
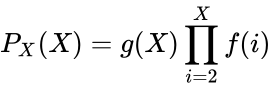
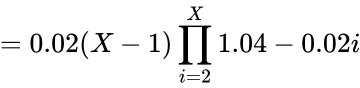
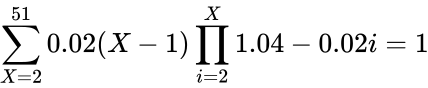
![{\displaystyle E[X]=\mu =\sum _{}^{k}kP_{X}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/png/0a2eba018cd52083b3774f0adbfa8ebb2c935f95)
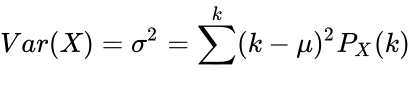
![{\displaystyle E[X]=\sum _{k=2}^{51}0.02k(k-1)\prod _{i=2}^{k}1.04-0.02i=9.54}](https://wikimedia.org/api/rest_v1/media/math/render/png/fcff34a54258736a7c58c911db88b2a5d74854c8)