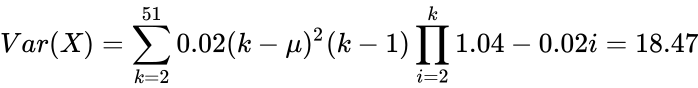Lockpick

| Type |
Relic |
|---|---|
| Index No. |
149/166 |
| Rarity |
Legendary |
| Shop |
900 |
| Minor Curse |
2 |
| Major Curse |
1 |
| Effect |
Open locks for free, but for how long? |
| GUID |
Item: 4cf72d4585f64a95b4d614bd559e4d58 |
![]() Lockpick is a relic item in UnderMine. It costs 2
Lockpick is a relic item in UnderMine. It costs 2 ![]() Minor Curses and 1
Minor Curses and 1 ![]() Major Curse at Sho'guul's lair.
Major Curse at Sho'guul's lair.
It unlocks doors, chests, and blocks without consuming the peasant's keys. Each time it is used its probability to break goes up by 2%. Its chance, in percentage, can be found on the relic's icon. The lockpick will still spare the use of a key when it breaks.
It can be combined with ![]() Lucky Charm to obtain the
Lucky Charm to obtain the ![]() Lucky Lockpick.
Lucky Lockpick.
On average, it is worth about 9.5 Keys (See derivation below).
The chance of the lockpick breaking can be reset to 0 by placing it on the Relic Altar and removing.
Interactions
Positive
 Lucky Charm: Combines into the
Lucky Charm: Combines into the  Lucky Lockpick.
Lucky Lockpick. Key Blade: More keys saved is more damage had with Key Blade.
Key Blade: More keys saved is more damage had with Key Blade.
Statistical Analysis of the Lockpick
A statistical analysis is useful for determining how many keys finding the lock pick will save you. The following sections will walk through the derivation and steps taken to determine the statistics behind the item.
Derivation of the Probability Density Function
Let X be the number of keys the lockpick saves the peasant. Since the lockpick saves the peasant a key even when it breaks, the minimum number of keys saved is 2 and the maximum number of keys saves is 51.
Therefore, X = {2, 3, …, 50, 51}.
In order to derive the average number of keys the lockpick will save the peasant, a probability density function (PDF) must be found. To derive this expression, let f(X) be the probability of the lockpick not breaking until the point of breaking for X number of saved keys. Similarly, let g(X) be the probability of the lockpick breaking for X number of saved keys. Constructed below is a table of f(X) and g(X) for early values of X.
| X | f(X) | g(X) |
|---|---|---|
| 2 | 1 | 0.02 |
| 3 | 0.98 | 0.04 |
| 4 | 0.96 | 0.06 |
| ... | ||
| 49 | 0.06 | 0.96 |
| 50 | 0.04 | 0.98 |
| 51 | 0.02 | 1.00 |
From the table, it is easy to see a linear relationship between the probabilities of breaking (or not breaking), and the amount of keys the lockpick has saved the peasant. These relationships can be expressed using:
Now that the probabilities of breaking and not breaking for the number of saved keys in known, it is possible to derive the PDF for the number of keys saved. The probability for saving X amount of keys is equal to the probability of the lockpick surviving X-1 times and breaking on the Xth try.
Therefore:
A quick check of the summation of probability across the entire sample space shows that the probability of all events is 1:
Mean and Variance
Now that the PDF of the amount of keys saved is known, all that is needed now is to apply the definitions of mean and variance.
Mean is calculated by:
Variance is calculated by:
Applying these definitions results in:
Thus, the lockpick, on average, will save the peasant 9.5 keys.
History
| Changelog | |
|---|---|
| Version | Additions and Changes |
| 0.3.0 |
|
| 0.3.1 |
|
Notes
- Will not replace key-based payment when buying something from Black Rabbit.



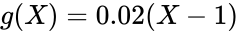
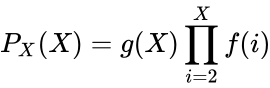
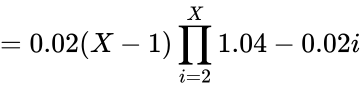
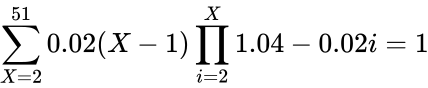
![{\displaystyle E[X]=\mu =\sum _{}^{k}kP_{X}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/png/0a2eba018cd52083b3774f0adbfa8ebb2c935f95)
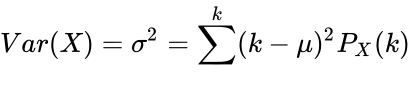
![{\displaystyle E[X]=\sum _{k=2}^{51}0.02k(k-1)\prod _{i=2}^{k}1.04-0.02i=9.54}](https://wikimedia.org/api/rest_v1/media/math/render/png/fcff34a54258736a7c58c911db88b2a5d74854c8)